Solving the Pocket Cube 2x2x2
Question: How many pieces do we need to solve?
Answer: 7 at the most! You can choose any piece and say: this is the one where I will begin solving the cube! In this way, the chosen piece becomes your basic one and according to that basic piece you will adjust and solve the other 7!
Question: Why 7 at the most? Can we start with fewer than 7?
Answer: You sure can! It is often the case that you start with 2 already solved pieces.
Question: Which colour should we begin with?
Answer: It is irrelevant, start with whatever suits you!
Question: Is it easy to learn the method of solving the Pocket Cube 2x2x2?
Answer: Yes, if you have already mastered the Rubik’s Cube 3x3x3, you already know how to solve the first layer. In step 2, there are only 7 algorithms for 7 different situations. In step 3, there are 2 optional algorithms for permuting the angles.
So, let us begin…
Step 1 – solving the first layer
For solving the first layer of the Pocket Cube 2x2x2, we will use the rotations you already know from solving the first layer of the Rubik’s Cube 3x3x3. Let us watch the following video that compares the rotations of these two cubes:
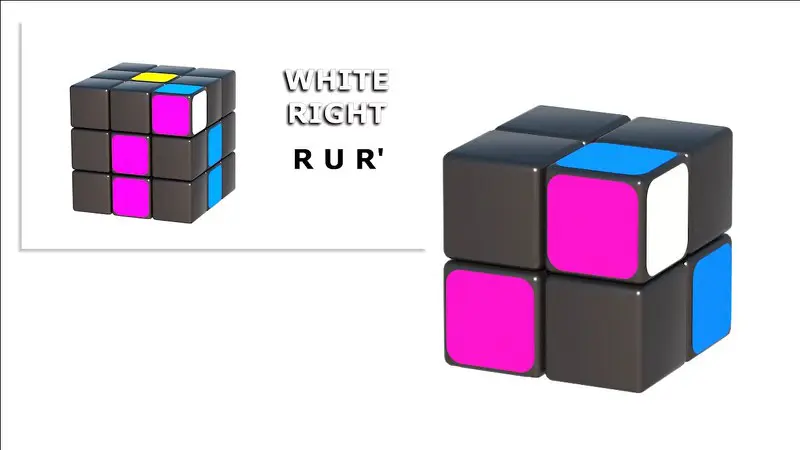
Let’s not forget that, prior to these rotations, the active piece from the upper row was led to the position upper-right, and that it is placed on the adequate side, considering its colors and the place where it should be placed.

Question: How are we to know whether the colors are adequate to these sides, and if it is on the adequate corner? There are no middle pieces that would determine the color of the sides!
Answer: True, there are no middle pieces here, and yet the chosen piece will be the one that determines the colors of these sides.

It is necessary to remember which are the colours of the opposing sides of the Pocket cube:
white - yellow
blue - green
red – purple (or orange)
Finally, for all of you who would like to solve the Pocket Cube 2x2x2 with as few moves as possible, the advice is to notice the neighboring side (↓ A) or diagonally matching pieces (↓ B) as shown in the following picture, and to base the future solving on them. Even if you do not come across these pieces at the start, we believe that in one or two moves, you will intuitively match two pieces that you see are easy to match! Try it!
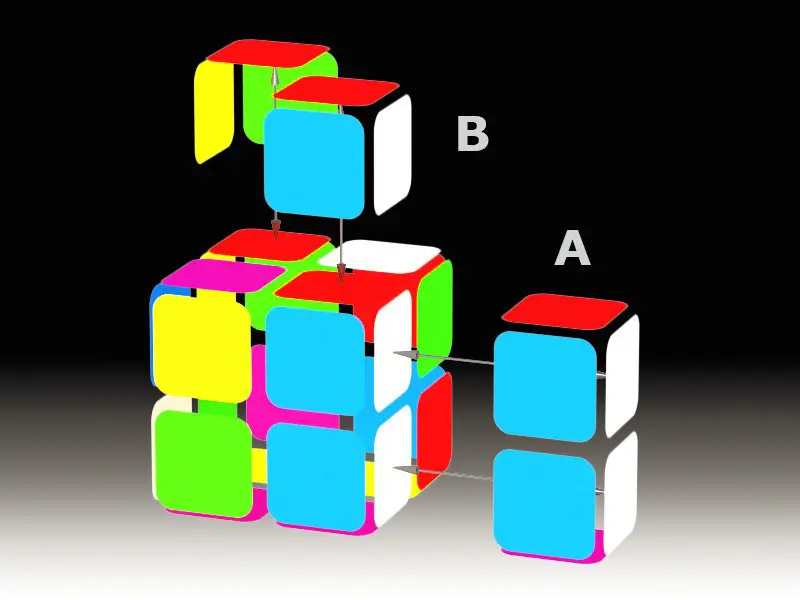
In the scenario ↑ A (this example) the starting color is either white or blue, and in the scenario ↑ B it is red. It is necessary to match the remaining two pieces of the first layer, and you can either do it intuitively, or in a classic way, based on the above-shown video.
(If you are an absolute beginner and find it hard to do this, simply start with the first piece that has a white color and match the other three, in a classic school way).
Solving the first layer is very easy; we have learnt to economize our moves, and to make any color the starting one.
Next step №. 2 - Learn to solve the color on the top of the Pocket Cube